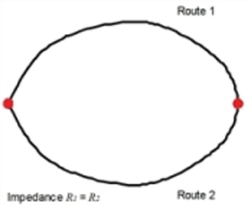
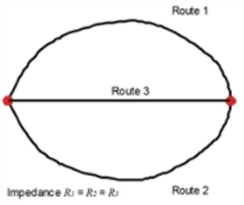
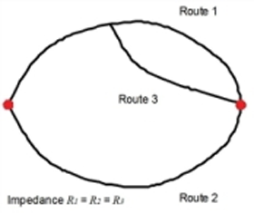
In the case of the stochastic assignment, alternative routes are generated - based on another assignment as initial solution - for an OD pair by varying the impedances of the network objects based on a distribution, in order to model the incomplete information supplied to the road-users and their individual differences in terms of perception and preferences. In this way, it is possible to calculate in one step not only the shortest route in terms of impedance, but also alternative routes with higher impedances. After completion of the route search, depending on the route impedance based on an assignment model (Logit, Box-Cox, Kirchhoff, Lohse or Lohse with variable beta), the demand is distributed across the alternatives. The similarity of the routes is to be taken into account during the distribution process. The problem of similarity is illustrated in the example below (Illustration 106):
Whereas the independence of the routes is given in cases 1 and 2, there is a dependency of the routes 1 and 3 in case 3, since there is some degree of overlap. This overlap must be taken into consideration in the route choice.
|
Case 1 |
|
Share |
|
|
|
|
expected |
Logit |
||
|
Route 1 |
50% |
50% |
||
|
Route 2 |
50% |
50% |
||
|
Case 2 |
|
Share |
|
|
|
|
expected |
Logit |
||
|
Route 1 |
33% |
33% |
||
|
Route 2 |
33% |
33% |
||
|
Route 3 |
33% |
33% |
||
|
Case 3 |
|
Share |
|
|
|
|
expected |
Logit |
||
|
Route 1 |
approx. 28% |
33% |
||
|
Route 2 |
approx. 44% |
33% |
||
|
Route 3 |
approx. 28% |
33% |
||
Illustration 106: Example of similarity of routes
The C-Logit approach proposed by CASCETTA is a suitable way of overcoming this problem. To do this, a so-called commonality factor C is introduced to measure the overlapping of the two routes r and s as follows:
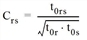 or
or 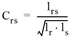
with
|
Crs |
Similarity of the routes r and s (Commonality factor) |
|
t0rs |
Time t0 of the common sections of the routes r and s |
|
t0r |
Time t0 of route r |
|
lrs |
Length l of the common sections of the routes r and s |
|
lr |
Length l of route r |
Thus, Crs equals 1, if the two routes are identical, and will be 0, if the two routes do not overlap. The commonality factor Crs is determined for all route combinations. Then, the correction factor CFr of a route r compared to any other route s is defined as follows:
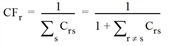
The correction factor of a route r is 1 if the commonality factors Crs for all routes s have the value 0, i.e. the route has no overlap with another route. In any other case it is below 1. The correction factor CFr is then accounted for in the Logit model as follows:
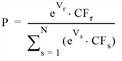
In the case of Box-Cox, Kirchhoff, Lohse or Lohse with variable beta, its inclusion is also carried out in the same way.
Alternatively, the correction factor CFr can be determined with a simpler approach according to Ben Akiva. It is then defined as:
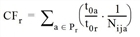
or
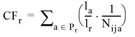
with
|
t0a |
Time t0 of link a |
|
t0r |
Time t0 of route r |
|
la |
Length l of link a |
|
lr |
Length l of route r |
|
Nija |
Number of routes of the OD pair ij that lead across link a |